- If ƒ¿ is greater than ƒÀ, A1 contains at least two different rational numbers, which are not contained in B1.
- If ƒÀ is greater than ƒ¿, B1 contains at least two different rational numbers, which are not contained in A1.
- If ƒ¿ equals ƒÀ, the results are divided into two cases. The first case, A1 is identical to B1. The second case, the difference between A1 and B1 is only one rational number, which equals ƒ¿ and ƒÀ. That is, these two Dedekind cuts are essentially identical.
Counting Dedekind Cuts
Next, we shall consider whether the number of irrational numbers is larger than that of rational numbers. Let us regard an irrational number as a pigeon and an interval of two rational numbers as a pigeonhole. According to the pigeonhole principle, if the number of irrational numbers were larger than that of rational numbers, there would be at least two irrational numbers, between which there is no rational number. However, there is no such a pair of irrational numbers, because there are at least two rational numbers between two different Dedekind cuts. That is, the number of irrational numbers is not larger than that of rational numbers. This is the first conclusion.Next, we shall consider another proof. Consider a real number ƒ¿ and the larger real number ƒÀ, and the difference of them equals ƒÃ:
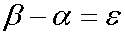
According to the axiom of Archimedes, no matter how small ƒÃ is, there exists a natural number such that:
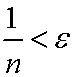
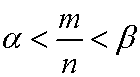
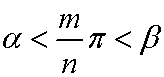
Furthermore, consider an arbitrary real number ƒÁ. The same logic as above can be applied to (m/n)ƒÁ. Then, there exists an integer m and a natural number n such that: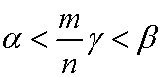
For an example, if we define ƒÎ as a unit, the magnitude nƒÎ corresponds to the natural number N: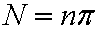
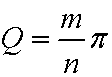
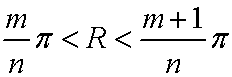
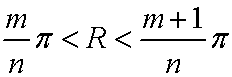
When we apply the Euclidean Geometry to the real world, we have to draw a line with a pencil or a printer. In both cases, there is the minimum dot. Even if we use any kind of tool, the minimum dot exists. So, we can only constitute a line from dots. That is, only the magnitude, which equals the Euclidean number, can be realized. So, the decision of the unit is important. When we actually use the Euclidean number, the unit is determined on a case-by-case basis. As a result, we can flexibly adapt the unit to the practical usage. Therefore, the Euclidean number system is sufficiently useful and does not cause contradictions.
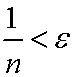
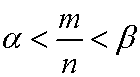
Contradictions
Next, the same logic as above can be applied to (m/n)ƒÎ. Then, there exists an integer m and a natural number n such that: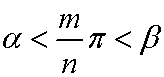
Furthermore, consider an arbitrary real number ƒÁ. The same logic as above can be applied to (m/n)ƒÁ. Then, there exists an integer m and a natural number n such that:
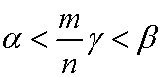
The Euclidean Number System
These contradictions mean that there is an error in the preconditions. At such case, it is best to return to the classic. We shall reread Euclid's Elements . Perhaps, Euclid might notice these contradictions, and then he described the solution. Firstly, a magnitude is defined as a length of a line segment in Book ‡X. Secondary, Euclid says "A number is a multitude composed of units" in the definition 2 of Book ‡Z. The difference between Euclid and Dedekind is evident. Dedekind regarded a magnitude as a number. In contrast, Euclid distinguishes the number from the magnitude. If we accept Euclid's standpoint, contradictions are eliminated.For an example, if we define ƒÎ as a unit, the magnitude nƒÎ corresponds to the natural number N:
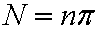
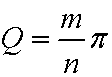
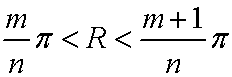
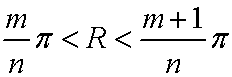
The Practical Usage of the Euclidean Number
Why does the number distinguish from the magnitude? If we want to count objects, we have to regard it as indivisible. Furthermore, if we have to count water, we pour water into bottles, and then we count bottles. That is, we can only count discrete and indivisible objects. At least, we have to regard the object as temporarily indivisible. Hence, we regard the magnitude, which consists of units, as the number.When we apply the Euclidean Geometry to the real world, we have to draw a line with a pencil or a printer. In both cases, there is the minimum dot. Even if we use any kind of tool, the minimum dot exists. So, we can only constitute a line from dots. That is, only the magnitude, which equals the Euclidean number, can be realized. So, the decision of the unit is important. When we actually use the Euclidean number, the unit is determined on a case-by-case basis. As a result, we can flexibly adapt the unit to the practical usage. Therefore, the Euclidean number system is sufficiently useful and does not cause contradictions.